While performing Linear Regression, we try to find out the best fit line (minimizing the error) through the data and calculate the slope and intercept of the line. (W and b respectively)

Fig. 1: Linear Regression best fit line
The basic Linear Regression algorithm that we are considering for data (X,Y) can be written in the following form:
Y = WT * X + b
where, W are the weights learned from the data, WT is the transpose of the W matrix and b is bias vector added to the equation. (in case the line does not pass through the origin)
Maximum likelihood Estimation of Model Parameters:
One way of solving the Linear Regression equation is to use Maximum Likelihood Estimation, In this, we find the value of model parameters (W and b) such that it maximizes the likelihood function, i.e. makes the data observed most probable.
Let probability of data given theta (parameters) be:
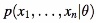
The more is this probability, the better is the theta (parameters) chosen. We have to maximize it. Hence,
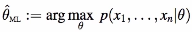
where theta (ML) is the maximum likelihood estimated value of the parameters.
Least Squares Estimation of Model Parameters:
In least squares, instead of maximizing the probability of the data for a given set of parameters, we try to minimize the value of the squared error for every data point observed. Error here is the difference between the true output value and the value predicted by the regression line estimated.
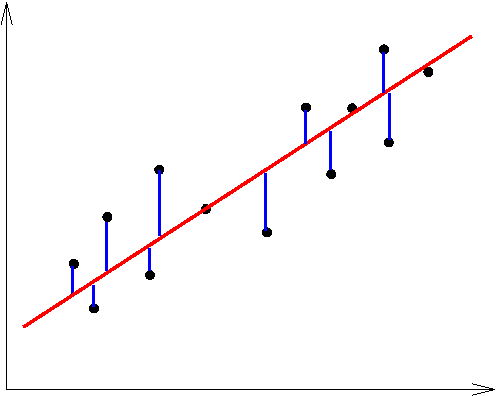
Fig. 2: Blue line is the error in estimation of the data (black point) by the regression line (red)
This leads to minimizing the following Loss function (sum of squared errors):
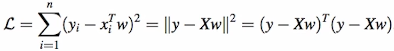
The solution for the above equation comes out to be :
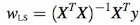
Also see: Geometry of Least Squares.
Ridge Regression
Ridge regression is a type of regularization technique which we used to limit the magnitude of W (penalize higher magnitude of w).
Why do we even need regularization?
Sometimes the variance of the results (or our model parameters) is so high that even with the small change in the input, the resuloting output changes a lot and becomes unstable (particularly when the input variables are correlated). By adding regularization term to the Loss function we make sure that the high values of W are penalized and this results into reduction of the variance of the output (although this adds bias to the result).
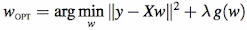
Ridge Regression is one way of adding regularization term g(w) where g(w) = ||w||^2. lambda here us called Regularization parameter. Greater the lambda, more is the loss, and since we have to minimize the loss, greater values of lambda leads to smaller values of w.
Note: If lambda = 0, this because equivalent to the Least Squares Solution.
It turns out, after solving for the above equation, the value of w is :
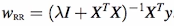
Maximum A Poseriori Estimation (MAP)
Maximum A Poseriori estimation seeks to find the most probable value of w under the posterior. In Maximum likelihood estimation, we found the value of w for which the observed data was most likely and we simply didn't involve any prior information of w which could be used.
By assuming that the prior of w a Guassian distribution with mean 0 and variance (lambda)^-1 and using Bayes Theorem,
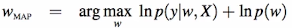
By solving it further for the value of w:

Some interesting relationships:
1) When we model the data points (xi, yi) in a linear model yi = xi.T*w, we can see that the least squares solution is equivalent to the maximum likelihood solution when y is assumed to have a Guassian distribution with mean Xw and variance (sigma^2 * I), which is given by:
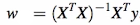
2) The solution of Wmap is equivalent to the Wrr (Ridge solution) on the condition to switching lambda to lambda*sigma^2.
From this we can conclude that the Ridge Regression maximizes the posterior, while Least Squares maximizes the likelihood.
And this is a quick introduction to some Regression techniques, intuition behind their working and relationships between them. Hope I have made the explanations clear.
Kush.